Prelab
For the prelab, I set up a debugging system that uses Bluetooth to send ToF data from the Artemis to my laptop. Because sending data from the Artemis to the laptop takes a non-negligible amount of time, this would make the control loop slower, leading to a less effective controller. Therefore, the strategy I used was to store all of the data on the Artemis’ memory and send it all at once after the task was over.
To do this, I created an array of length 1000, which would be large enough to store 5 seconds of timestamped ToF sensor data. Then every time I looped through the control loop, I appended the current time and the current distance. At the end of the task, I looped through this array and sent each element in the array one by one via Bluetooth. The following is the code I wrote to achieve this:
Lab Tasks
P Controller
I first chose to implement a P (proportional) controller. To implement a P controller, I first set a target distance (a.k.a. reference input in control theory) of 300 mm. That is, the goal is to have the robot stop at a distance 300 mm from the wall. The error is defined as the current distance minus the target distance. And to reach the target distance as fast as possible, the input is made to be proportional to the error — that is, the larger the error, the larger the input. Then this input is inputted into the motor. The value of Kp was determined through trial and error. Here is the code for implementing a P controller:
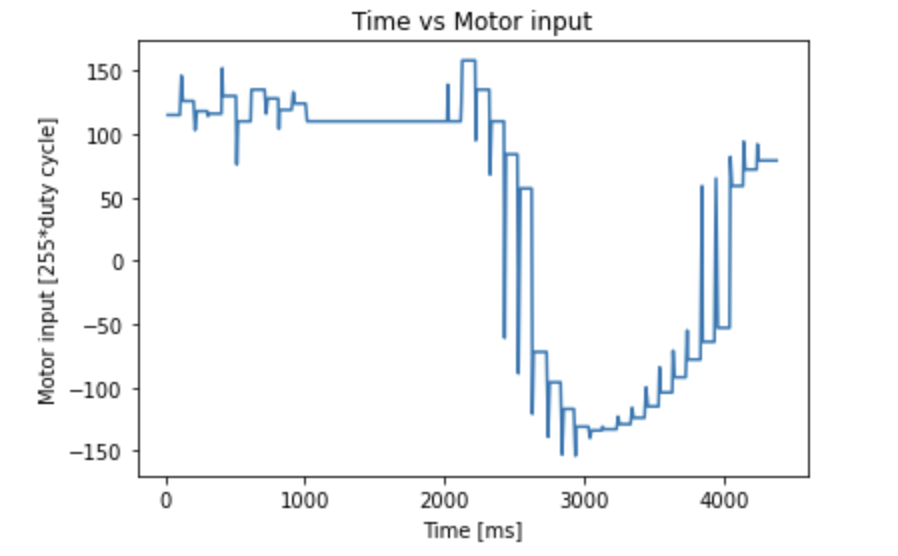
When the PID value is between -110 and 110, I added 50 to overcome the motor’s deadzone. When the absolute value of the PID value is greater than 110, I capped off the motor input at 110 because it will crash into the wall even with the controller in place.
The code for the helper functions used (forward() and backward()) is the following:
Here is a video of the robot running on the PD controller:
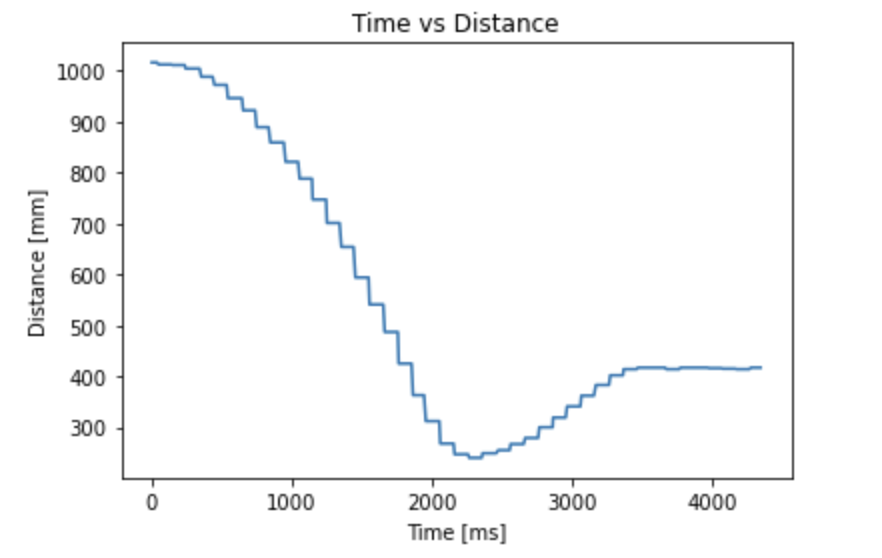
As you can see, the robot overshoots passed the target distance and is unable to stop in time and hits the wall. No matter how much I lowered the Kp value, the robot seemed to crash into the wall (I found the reason why which will be explained in the next section). This motivated me to add a derivative term to the controller.
PD Controller
Adding a derivative term has the effect of preventing an overshoot by easing up the control input as the robot approaches the target distance. To implement a PD controller, I had to modify the code so that it keeps track of the error from the previous loop. Then I calculated the change in error by computing the current error minus the previous error. I scaled this difference by a constant Kd and added this to the proportional term. The value of Kd was increased until the robot was no longer crashing into the wall. Here is the code that implements a PD controller:
Here is a video of the robot running on the PD controller:
Adding the derivative term successfully prevented the robot from overshooting and hitting the wall.
Here is a plot of time vs. distance (from the wall):
And here is a plot of time vs. motor input: